

Starting concentration now, what's half of that? So on our graph half of How long does it take to do that? Well if this is our How long does it takeįor the second half-life? So how long does it take to go from four molecules to two molecules? Let me go ahead and changeĬolor and be consistent here. So we find that point on our graph and we drop down to here on the x-axis and it took one second.
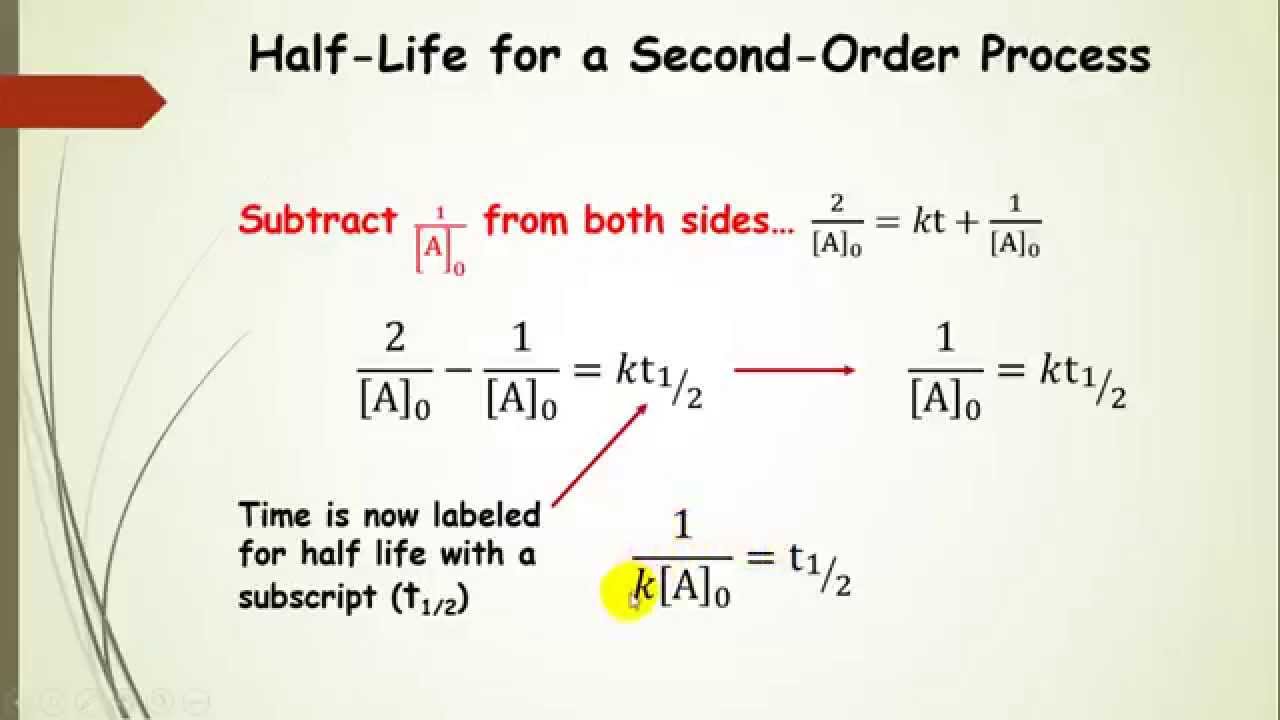
That would be the initialĬoncentration of A divided by two. The initial concentration, half that would be right here. To go from eight to four? Alright we can find that on our graph. Alright so we're left with four molecules so I'll draw those in there and how long did it take Alright, so if we waitįor the concentration to decrease to half its initial, what are we left with? We were left with four molecules. With eight particles that are eight molecules so here we have one, two, three, four, five, six, seven, eight. And let's just do a made-up reaction here. So here is our initial concentration of A. On the graph would be the initial concentration of A. So when time is equal to zero, alright, this point right here Of concentration versus time for a second order reaction so we can understand this conceptĪ little bit better. For a first order reaction we saw that the half-life was constant but here the half-life isn't constant because the half-life depends on the initial concentration of A. Notice this is very different for the half-life for a first order reaction. And so here's our equation for the half-life for a second order reaction. So we get the half-life is equal to one over k times the initial concentration of A.

The initial concentration of A and that's equal to the rate constant k times the half-life. Initial concentration of A minus one over the initialĬoncentration of A? That would just be one over Initial concentration of A is equal to k t1/2. So one the left side this would just be two over the initial concentration of A minus one over the Initial concentration of A divided by two minus one over the initial concentration of A is equal to the rate constant k times the half-life. So it's half of our initial concentration. So our initialĬoncentration would be this. T 1/2 in for the time what's the concentration of A? Well using the definition for half-life, the concentration of A should be half of the initial concentration. Time is equal to t 1/2 so we're going to plug So if we're talking about the half-life so that would be when One over the concentration of A minus one over the initial concentration of A is equal to the rateĬonstant k times the time. Integrated rate equation for a second order reaction. We've also already talked about the integrated rate law or the Time that it takes for the concentration ofĪ reactant to decrease to half of its initial concentration. Remember half-life is symbolized by t 1/2. t will yield a straight line with slope k and intercept 1/ o, as shown below. The above equation is the integrated rate law with the form y = mx +c. Rearranging and integrating the above equation gives the integrated rate law.

Since the reaction rate is the negative time derivative of concentration, the differential form of the rate law can be written as follows. Therefore, the unit for the rate constant is mol -1 Solving for the unit of the rate constant k gives The unit for the reaction rate is moles per liter per second or mol L -1 s -1, and the concentration unit is moles per liter or mol L -1. Type 2: One molecule each of two reactants and reacts to give products. If the concentration is reduced by one-half, the rate is reduced by one-fourth. Note that if the concentration is doubled, the rate is quadrupled. This type of reaction is common in dimerization, where two monomers combine to form a polymer. Where is the concentration and k is the rate constant.


 0 kommentar(er)
0 kommentar(er)
